11. Statistik#
Im Laufe der Kapitel haben wir bereits einige Datensätze betrachtet. Einen wichtigen Aspekt haben wir aber bisher ignoriert: die Rolle des Zufalls, um Unterschiede zu erklären. Daher wollen wir uns an dieser Stelle noch mit Methoden aus der Statistik beschäftigen, die dazu geeignet sind, Aussagen darüber zu treffen, ob wir einen echten Effekt beobachten oder lediglich zufällige Schwankungen. Um zu verstehen, warum das relevant ist, betrachten wir direkt zwei Beispiele. In Kapitel 4 haben wir zum Beispiel die Verteilung von Daten mit Histogrammen visualisiert. Hier sind die Histogramme von zwei weiteren Datensätzen:
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# generate data
np.random.seed(42)
mu, sigma = 0, 0.2 # mean and standard deviation
s1 = np.random.normal(mu, sigma, 200)
s2 = np.random.normal(mu+0.05, sigma, 200)
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].hist(s1, 30, density=True, alpha=0.5)
axes[0].set_title("Histogramm von zufällig generierten Daten\nFrage: Sind diese Daten normalverteilt?")
axes[0].set_xlabel("x")
axes[0].set_ylabel("count")
axes[1].hist(s1, 30, density=True, alpha=0.5)
axes[1].hist(s2, 30, density=True, alpha=0.5)
axes[1].set_title('Histogramm von zufällig generierten Daten\nmean("blau"): %.2f - mean("orange"): %.2f\nFrage: Sind die Mittelwerte verschieden?' % (np.mean(s1), np.mean(s2)))
axes[1].set_xlabel("x")
axes[1].set_ylabel("count")
plt.show()
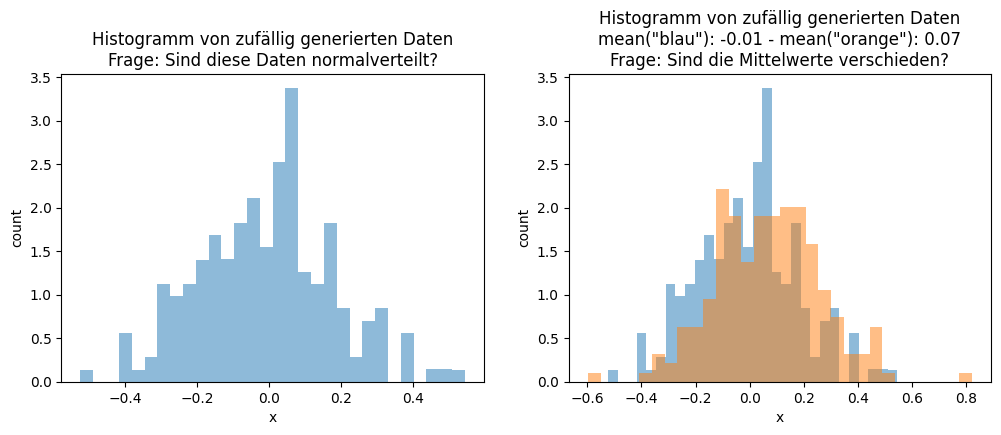
Das Histogramm auf der linken Seite hat eine Glockenform, was auf eine Normalverteilung hindeutet. Wie wahrscheinlich es ist, dass es sich um eine Normalverteilung handelt, ist jedoch unklar. Auf der rechten Seite sehen wir die Histogramme von zwei Stichproben \(X_1 = \{x_1^1, ..., x_{n_1}^1\}\) (“blau”) und \(X_2 = \{x_1^2, ..., x_{n_2}^2\}\) (“orange”). Diese Stichproben sind aus der “blauen” und der “orangen” Grundgesamtheit gezogen, die auch Populationen genannt werden. Beide Stichproben sehen sich sehr ähnlich, auch wenn der Mittelwert der blauen Daten etwas kleiner ist als bei den orangen Daten. Ob dies ein zufälliger Effekt der Stichproben ist oder ob die blaue Population im Mittel wirklich etwas kleiner ist, kann man mit dem Histogramm nicht erkennen.
Statistische Methoden können uns diese Fragen (mit einer gewissen Wahrscheinlichkeit) beantworten. In diesem Kapitel befassen wir uns in einer kurzen Einführung mit der ziemlich großen Welt der Statistik. Unser Ziel ist ein Grundverständnis von Hypothesentests, Effektstärken und Konfidenzintervallen. Die Hypothesen in diesem Kapitel sind nicht mit den Hypothesen eines Klassifikationsmodells zu verwechseln (siehe Kapitel 8).
11.1. Hypothesentests#
Hypothesentests sind das wichtigste Werkzeug der häufigkeitsbasierten Statistik (engl. frequentist statistics). Bei Hypothesentests hat man Annahmen an die Daten. Durch diese Annahmen kann man Hypothesen über die Daten formulieren. Es gibt immer zwei Hypothesen: die Nullhypothese und die Alternativhypothese.
Nullhypothese (\(H_0\)): Die Annahmen des Tests sind erfüllt und können nicht mit einem vorgegebenen Signifikanzniveau verworfen werden.
Alternativhypothese (\(H_1\)): Die Annahmen des Tests sind nicht erfüllt und können mit einem vorgegebenen Signifikanzniveau verworfen werden.
Die Formulierung dieser Hypothesen basiert auf einigen abstrakten Konzepten: Was genau ist eine “Annahme” und was heißt “mit einem vorgegebenen Signifikanzniveau verwerfen”? Im Folgenden erklären wir die Bedeutung dieser Konzepte am Beispiel des \(t\)-Tests.
11.1.1. \(t\)-Test#
Der \(t\)-Test ist der Urvater der statistischen Tests und wurde von William Gosset unter dem Pseudonym “Student” entwickelt. Die älteste Version des Tests und die Wahrscheinlichkeitsverteilung, auf dem dieser Test basiert, heißen daher auch Students \(t\)-Test und Students \(t\)-Verteilung. Wir betrachten hier eine neuere Variante des \(t\)-Tests, nämlich Welchs \(t\)-Test. Welchs \(t\)-Test hat folgende Hypothesen:
\(H_0\): Die Mittelwerte von zwei normalverteilten Populationen \(X_1\) und \(X_2\) sind gleich.
\(H_1\): \(X_1\) und \(X_2\) sind keine normalverteilten Populationen mit dem gleichen Mittelwert.
Anhand der Hypothesen kann man bereits den Zweck des \(t\)-Tests erkennen: Wir wollen bestimmen können, ob die Mittelwerte unterschiedlich sind. Zum besseren Verständnis hier ein Beispiel: Wir wollen wissen, ob das Durchschnittsalter der Einwohner von Berlin gleich dem von Hamburg ist. In beiden Städten haben wir 10.000 Einwohner zufällig ausgewählt und nach dem Alter gefragt. Die Städte sind unsere Populationen, die ausgewählten Einwohner unsere Stichproben. Derartige Fragestellungen gibt es häufig: Sind zwei Medikamente gleich wirksam oder auch ist mein Random Forest gleich gut wie mein neuronales Netz?
Eine wichtige Eigenschaft vom \(t\)-Test ist, dass die Alternativhypothese nicht aussagt, dass die Mittelwerte nicht gleich sind. Sie sagt lediglich aus, dass wenn \(X_1\) und \(X_2\) beide normalverteilt sind, die Mittelwerte unterschiedlich sind. Wenn eine von beiden Populationen nicht normalverteilt ist, weiß man nicht, ob die Nullhypothese verworfen wurde, weil die Mittelwerte unterschiedlich sind oder weil es keine Normalverteilung war. Diese wichtige Eigenschaft wird oft vergessen und ist einer der häufigsten Fehler bei der Benutzung von Hypothesentests.
Der \(t\)-Test bestimmt, ob die Nullhypothese verworfen wird, basierend auf der Überlegung, wie wahrscheinlich es ist, die Stichprobe zu beobachten, wenn die Hypothese zutrifft. Für den \(t\)-Test heißt das, dass man berechnet, wie wahrscheinlich es ist, die Stichproben \(X_1\) und \(X_2\) zu beobachten, wenn beide aus normalverteilten Populationen mit dem gleichen Mittelwert gezogen werden. Dies ist der gleichermaßen berühmte wie berüchtigte p-value. Um den p-value zu bestimmen, brauchen wir eine Teststatistik. Im Fall vom \(t\)-Test ist das Students \(t\)-Verteilung.
Show code cell source
from scipy import stats
rv = stats.t(df=100, loc=0, scale=1)
x = np.linspace(rv.ppf(0.0001), rv.ppf(0.9999), 100)
y = rv.pdf(x)
fig, ax = plt.subplots()
ax.set_title("Students $t$-Verteilung mit 100 Freiheitsgraden")
ax.set_xlim(-5, 5)
ax.plot(x, y)
plt.show()
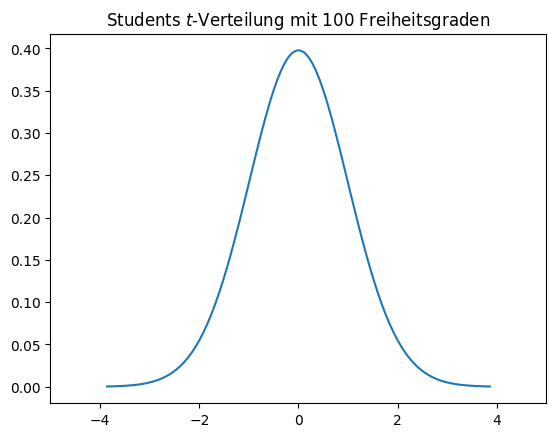
Diese Verteilung sieht auf den ersten Blick aus wie eine Normalverteilung. Die \(t\)-Verteilung hat jedoch eine etwas breitere Glocke als die Normalverteilung, die Fläche ist also in den Randbereichen größer. Diese Ähnlichkeit zur Normalverteilung ist kein Zufall. Die \(t\)-Verteilung ist definiert als die erwartete Abweichung des Mittelwerts von null bei einer Stichprobe, die aus der Standardnormalverteilung mit Mittelwert null und Standardabweichung eins gezogen wurde. Die \(t\)-Verteilung sagt also etwas über die Unsicherheit der Mittelwerts einer Stichprobe aus. Diese Unsicherheit können wir natürlich auch für zwei Stichproben bestimmen, was dann schon sehr ähnlich zu unserer Hypothese ist.
Der Unterschied ist, dass die \(t\)-Verteilung die Unsicherheit für einen Mittelwert von null und eine Standardabweichung von eins berechnet, wir aber mit unserer Hypothese beliebige Normalverteilungen zulassen. Daher benötigen wir die Teststatistik. Diese ist für den \(t\)-Test definiert als
Diese Gleichung sieht zwar kompliziert aus, ist aber - etwas vereinfacht ausgedrückt - nichts anderes als eine Standardisierung der Stichproben, sodass sich die Differenz der Mittelwerte wie bei zwei Standardnormalverteilungen verhält. Daher können wir die \(t\)-Verteilung benutzen, um auszurechnen, wie wahrscheinlich es ist, dass wir diese Abweichung beobachten. Hierfür berechnet man die Fläche unter der \(t\)-Verteilung außerhalb von \(\pm t\).
Show code cell source
tvalue = 2
xfill = np.linspace(-tvalue, tvalue)
xfill_left = np.linspace(rv.ppf(0.0001),-tvalue)
xfill_right = np.linspace(rv.ppf(0.9999),tvalue)
plt.figure()
plt.title("p-value mit Students $t$-Verteilung\nDie grüne Fläche ist der p-value")
plt.axvline(tvalue, linestyle=':')
plt.axvline(-tvalue, linestyle=':')
plt.xlim(-5,5)
plt.xticks([-tvalue,0,tvalue], ['-t','0','t'])
plt.plot(x,y)
plt.fill_between(xfill, rv.pdf(xfill), y2=0, alpha=0.1, color='b')
plt.fill_between(xfill_left, rv.pdf(xfill_left), y2=0, alpha=0.2, color='g')
plt.fill_between(xfill_right, rv.pdf(xfill_right), y2=0, alpha=0.2, color='g')
plt.show()
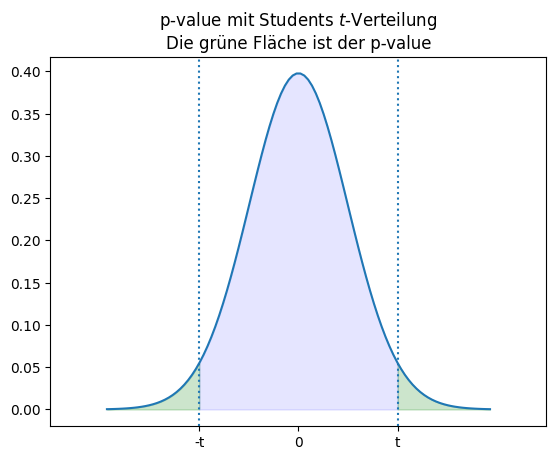
Die grüne Fläche ist die Wahrscheinlichkeit, dass die Stichprobe einer Standardnormalverteilung um mindestens \(t\) von null abweicht. Da wir \(t\) so berechnen, dass es genau die Abweichung der Mittelwerte voneinander darstellt, entspricht dies der Wahrscheinlichkeit, dass die zwei Stichproben gezogen wurden, wenn die Populationen normalverteilt sind und den gleichen Mittelwert haben. Das ist der p-value des \(t\)-Tests: Die Wahrscheinlichkeit, dass die Daten beobachtet werden, wenn unsere Nullhypothese zutrifft.
11.1.2. Das Signifikanzniveau#
Der p-value gibt also an, wie wahrscheinlich es ist, die Daten zu sehen. Es ist also nur logisch, dass ein kleiner p-value darauf hindeutet, dass die Nullhypothese nicht zutrifft und verworfen werden sollte. Diese Folgerung wird durch das Signifikanzniveau \(\alpha\) formalisiert, um die statistische Signifikanz des Testergebnisses zu definieren. Das Signifikanzniveau ist definiert als die Wahrscheinlichkeit, dass die Nullhypothese verworfen wird, obwohl sie zutrifft. Häufig wird ein Signifikanzniveau von 0,05 oder in letzter Zeit auch 0,005 verwendet. Mit dem Signifikanzniveau können wir anhand von p-value entscheiden, ob wir die Nullhypothese verwerfen:
Wenn \(\text{p-value} > \alpha\) ist, können wir die Nullhypothese nicht verwerfen. Das heißt, dass die Stichproben nicht unwahrscheinlich sind, wenn die Nullhypothese wahr ist.
Wenn \(\text{p-value} \leq \alpha\) ist, verwerfen wir die Nullhypothese und haben ein statistisch signifikantes Ergebnis. Die Stichproben sind also sehr unwahrscheinlich, wenn die Nullhypothese wahr ist.
Mit Hypothesentests erhält man keine absolute Sicherheit, die Ergebnisse stimmen nur mit einer durch das Signifikanzniveau festgelegten Wahrscheinlichkeit. Das heißt auch, dass wenn wir die Nullhypothese verwerfen, sie trotzdem wahr sein könnte. Es ist nur unwahrscheinlich - aber nicht unmöglich! -, dass diese Daten vorkommen. Deshalb verwenden wir auch die etwas komplizierten Formulierungen nicht verwerfen können bzw. verwerfen bezogen auf ein Signifikanzniveau.
11.1.3. Wichtige Hypothesentests#
Was wir oben im Detail für den \(t\)-Test erklärt haben, gilt für alle statistischen Tests: Es gibt eine Nullhypothese, in der wir Annahmen treffen. Dann berechnen wir den p-value, also die Wahrscheinlichkeit der Daten, entsprechend den Annahmen. Basierend auf dem p-value können wir bestimmen, ob wir die Nullhypothese mit einem gewissen Signifikanzniveau verwerfen. Es gibt sehr viele derartige statistische Tests. Hier sind die Nullhypothesen einiger sehr wichtiger Tests:
Welchs \(t\)-Test: Die Mittelwerte zweier unabhängiger normalverteilter Populationen sind gleich.
Mann-Whitney-U-Test / Wilcoxon-Ranksum-Test: Die Werte einer Population dominieren die Werte einer anderen Population nicht (entspricht in etwa der Frage, ob die Mediane gleich sind).
Shapiro-Wilk-Test: Die Population einer Stichprobe mit einer Größe zwischen 3 und 5.000 ist normalverteilt.
Levene-Test: Die Varianz von einer Gruppe von Populationen ist gleich.
ANOVA (F-Test): Die Mittelwerte einer Gruppe von normalverteilten Populationen mit gleichen Varianzen sind gleich.
Kolmogorow-Smirnow-Test: Zwei Populationen haben die gleiche Wahrscheinlichkeitsverteilung.
Wir wissen bereits, dass wir Welchs \(t\)-Test benutzen können, um die Mittelwerte von Normalverteilungen zu vergleichen. Wenn die Daten nicht normalverteilt sind, können wir stattdessen den Mann-Whitney-U-Test nutzen. Mithilfe des Shapiro-Wilk-Tests können wir bestimmen, ob eine Stichprobe normalverteilt ist. Wenn man mehr als zwei Datensätze vergleichen möchte, spricht man von einer Gruppe von Populationen. Mit ANOVA kann man bestimmen, ob die Mittelwerte aller dieser Populationen gleich sind, sofern es sich um Normalverteilungen mit der gleichen Varianz handelt. Die Normalverteilung können wir mit dem Shapiro-Wilk-Test überprüfen, für die Varianzen können wir den Levene-Test verwenden.
Ähnlich wie bei den deskriptiven Statistiken (siehe Kapitel 4) gibt es parametrische und nicht parametrische statistische Tests. Die parametrischen Tests haben Annahmen an die Daten (z.B. Normalverteilung), die nicht parametrischen Tests machen keine derartigen Annahmen. Welchs \(t\)-Test ist zum Beispiel parametrisch und der Mann-Whitney-U-Test ist das nicht parametrische Gegenstück.
Der Kolmogorow-Smirnow-Test ist ein sehr generischer statistischer Test, da er beliebige Populationen mit kontinuierlichen Verteilungen miteinander vergleichen kann. Es gibt also nur wenige Einschränkungen, wann man den Test benutzen kann. Dennoch sollte man ihn als “letztes Mittel” betrachten, mit dem man zumindest sagen kann, ob es irgendwelche Unterschiede gibt. Was genau unterschiedlich ist, zum Beispiel die Lage, die Variabilität oder die Art der Verteilung, ist unklar. Als Vergleich: Wenn man mit dem Shapiro-Wilk-Test bestimmt, dass die Populationen normalverteilt sind, und mit Welchs \(t\)-Test einen signifikanten Unterschied der Mittelwerte feststellt, weiß man sehr genau, wie sich die Populationen voneinander unterscheiden.
11.1.4. Anwendung der Tests#
Mit dem uns jetzt bekannten Wissen über die statistischen Tests können wir die Fragen vom Anfang des Kapitels beantworten: Sind die Mittelwerte der blauen und der orangen Population unterschiedlich? Mithilfe der Hypothesentests können wir hierzu eine Aussage treffen, die mit hoher Wahrscheinlichkeit richtig ist. Hierzu müssen wir ein Signifikanzniveau \(\alpha\) festlegen. Anschließend können wir den Shapiro-Wilk-Test auf beide Stichproben anwenden, um zu bestimmen, ob die Populationen normalverteilt sind. Wenn dies der Fall ist, können wir die Mittelwerte mit Welchs \(t\)-Test vergleichen, ansonsten nehmen wir den Mann-Whitney-U-Test.
Show code cell source
from textwrap import TextWrapper
wrapper = TextWrapper(width=65)
def wrap_print(string):
print('\n'.join(wrapper.wrap(string)))
alpha = 0.05
pval_shapiro1 = stats.shapiro(s1)[1]
pval_shapiro2 = stats.shapiro(s2)[1]
wrap_print('p-value des Shapiro-Wilk-Tests für die "blauen" Daten: %.4f' % pval_shapiro1)
if pval_shapiro1>alpha:
wrap_print('Der Test hat ermittelt, dass die Daten wahrscheinlich normalverteilt sind, und wir können die Nullhypothese nicht mit einem Signifikanzniveau von alpha=%.3f verwerfen.' % alpha)
else:
wrap_print('Der Test hat ermittelt, dass die Daten wahrscheinlich nicht normalverteilt sind, und wir verwerfen die Nullhypothese mit einem Signifikanzniveau von alpha=%.3f.' % alpha)
print()
print('p-value des Shapiro-Wilk-Tests für die "orangen" Daten: %.4f' % pval_shapiro2)
if pval_shapiro1>alpha:
wrap_print('Der Test hat ermittelt, dass die Daten wahrscheinlich normalverteilt sind, und wir können die Nullhypothese nicht mit einem Signifikanzniveau von alpha=%.3f verwerfen.' % alpha)
else:
wrap_print('Der Test hat ermittelt, dass die Daten wahrscheinlich nicht normalverteilt sind, und wir verwerfen die Nullhypothese mit einem Signifikanzniveau von alpha=%.3f.' % alpha)
print()
if pval_shapiro1>alpha and pval_shapiro2>alpha:
wrap_print("Beide Populationen sind normalverteilt. Wir benutzen Welch's t-Test.")
pval_equal = stats.ttest_ind(s1,s2,equal_var=False)[1]
print()
wrap_print("p-value von Welchs t-Test: %f" % pval_equal)
if pval_equal>alpha:
wrap_print('Der Test hat ermittelt, dass die Mittelwerte wahrscheinlich gleich sind, und wir können die Nullhypothese nicht mit einem Signifikanzniveau von alpha=%.3f verwerfen.' % alpha)
else:
wrap_print('Der Test hat ermittelt, dass die Mittelwerte wahrscheinlich nicht gleich sind, und wir verwerfen die Nullhypothese mit einem Signifikanzniveau von alpha=%.3f.' % alpha)
else:
wrap_print("Mindestens eine Population ist nicht normalverteilt. Wir benutzen den Mann-Whitney-U-Test.")
pval_equal = stats.mannwhitneyu(s1,s2,alternative='two-sided')[1]
wrap_print("p-value des Mann-Whitney-U Tests: %f" % pval_equal)
if pval_equal>alpha:
wrap_print('Der Test hat ermittelt, dass die Populationen sich nicht dominieren, und wir können die Nullhypothese nicht mit einem Signifikanzniveau von alpha=%.3f verwerfen.' % alpha)
else:
wrap_print('Der Test hat ermittelt, dass eine Population die andere dominiert, und wir verwerfen die Nullhypothese mit einem Signifikanzniveau von alpha=%.3f.' % alpha)
p-value des Shapiro-Wilk-Tests für die "blauen" Daten: 0.8290
Der Test hat ermittelt, dass die Daten wahrscheinlich
normalverteilt sind, und wir können die Nullhypothese nicht mit
einem Signifikanzniveau von alpha=0.050 verwerfen.
p-value des Shapiro-Wilk-Tests für die "orangen" Daten: 0.2498
Der Test hat ermittelt, dass die Daten wahrscheinlich
normalverteilt sind, und wir können die Nullhypothese nicht mit
einem Signifikanzniveau von alpha=0.050 verwerfen.
Beide Populationen sind normalverteilt. Wir benutzen Welch's
t-Test.
p-value von Welchs t-Test: 0.000102
Der Test hat ermittelt, dass die Mittelwerte wahrscheinlich nicht
gleich sind, und wir verwerfen die Nullhypothese mit einem
Signifikanzniveau von alpha=0.050.
Die Tests haben also festgestellt, dass die Daten wahrscheinlich normalverteilt sind, aber die Mittelwerte nicht gleich sind. Wir haben also einen statistisch signifikanten Unterschied zwischen den blauen und den orangen Daten mit einem Signifikanzniveau von \(\alpha=0.05\).
11.1.5. Übliche Fehler bei Hypothesentests#
Bei Hypothesentests steckt der Teufel im Detail, da es viele Aspekte gibt, die man vergessen oder ungenau darstellen kann, was dazu führen kann, dass man die Ergebnisse überinterpretiert. Daher wollen wir hier einige größere und häufig vorkommende Fehler nennen, damit wir diese vermeiden können.
Das größte Problem ist, dass man Hypothesentests nutzt, um binäre Aussagen zu machen, zum Beispiel “die Daten sind normalverteilt” statt “der statistische Test indiziert, dass die Daten mit hoher Wahrscheinlichkeit normalverteilt sind”. Der große Unterschied: Die korrekte Aussage beinhaltet, dass es eine gewisse Unsicherheit über das Ergebnis gibt, was bei der absoluten Aussage nicht der Fall ist. Dass derartige Fehler (häufig!) passieren, ist verständlich. Das korrekte Formulieren von statistischen Ergebnissen ist schwierig und die Sätze klingen oft umständlich, was dazu verleitet, lieber eine deutlich einfachere absolute Formulierung zu benutzen.
Ein weiteres Problem ist, dass p-values häufig falsch benutzt werden. Dies liegt daran, dass die Definition von p-value als die Wahrscheinlichkeit, die Daten unter den gegebenen Annahmen zu beobachten, relativ komplex ist. Aus diesem Grund gibt es auch viele Forscher, die am liebsten Hypothesentests komplett abschaffen und durch andere Verfahren (Bayesian Statistics) ersetzen würden. Es gibt aber auch sehr viele Forscher, die das Problem in der falschen Verwendung der p-values sehen, sodass lediglich eine bessere Statistikausbildung erforderlich ist. In diesem Sinne betrachten wir hier auch die zwei größten Probleme der p-values: Scoring und p-Hacking.
Scoring bedeutet, dass der p-value als Punktzahl interpretiert wird und dann die Unterschiede der Populationen anhand ihrer p-values sortiert werden. Dies macht jedoch keinen Sinn, da die p-values eben nicht die Wahrscheinlichkeit, dass eine Hypothese korrekt ist, schätzen, sondern nur, dass die Daten zur Annahme passen. Eine Sortierung wäre also stattdessen eine Art Bewertung der Daten, was nicht gewollt ist.
Das p-Hacking passiert oft unbewusst. Auch hier liegt das Problem daran, dass die p-values die Wahrscheinlichkeit sind, dass die Daten unter Berücksichtigung der Annahmen generiert werden. Ein p-value von 0,05 bedeutet also, dass es eine 5%ige Wahrscheinlichkeit gibt, dass diese Daten generiert werden, unter der Annahme, dass die Nullhypothese zutrifft. Mit anderen Worten, es wird vom Test sogar erwartet, dass es eine gewisse Anzahl von falsch-positiven Testergebnissen gibt, also dass wir die Nullhypothese verwerfen, obwohl diese zutrifft. Dies ist im Allgemeinen kein Problem, solange die Wahrscheinlichkeit hierfür niedrig ist. Wenn man jedoch 20 Tests durchführt und jeder Test mit 5% Wahrscheinlichkeit falsch-positiv ist, ist es fast sicher, dass es falsch-positive Ergebnisse gibt. Diesem Effekt kann man entgegenwirken, indem man ein höheres Signifikanzniveau verlangt, was bedeutet, dass der p-value zum Verwerfen der Hypothesen kleiner sein muss, wodurch man die Wahrscheinlichkeit von falsch-positiven Ergebnissen reduziert. Man spricht hierbei auch vom p-value adjustment, zum Beispiel durch die Bonferonni-Korrektur [1]. Derartiges p-Hacking ist oft keine Absicht, sondern geschieht durch die Analyse von Teilgruppen. Um zu unserem Beispiel vom Alter der Einwohner zurückzukommen: Auch wenn Berlin und Hamburg das gleiche Durchschnittsalter hätten, würde man sehr sicher Stadtteile finden, wo die Abweichung größer wäre und der Unterschied dadurch signifikant. Ein berühmtes Beispiel dafür ist dieser medizinische Fachartikel [2]: Die Autoren wurden von den Herausgebern gezwungen, Teilgruppen zu analysieren. Um zu demonstrieren, dass dies zu falsch-positiven Ergebnissen führt, haben sie auch eine Analyse der Auswirkungen der Sternzeichen auf die Behandlung mit aufgenommen.
11.2. Effektstärke#
Die Signifikanz von Ergebnissen bedeutet nicht immer, dass ein Unterschied auch eine Bedeutung hat. Für unsere blauen und orangen Daten haben wir folgende Mittelwerte und Standardabweichungen:
Show code cell source
print('mean("blue") = %.2f' % np.mean(s1))
print('sd("blue") = %.2f' % np.std(s1))
print('mean("orange") = %.2f' % np.mean(s2))
print('sd("orange") = %.2f' % np.std(s2))
mean("blue") = -0.01
sd("blue") = 0.19
mean("orange") = 0.07
sd("orange") = 0.20
Der Unterschied der Mittelwerte ist im Verhältnis zu Standardabweichung also sehr klein. Die Effektstärke erweitert das Konzept der Signifikanz mit einem Maß dafür, wie groß die Differenz ist. Für normalverteilte Daten kann die Effektstärke für den Unterschied der Mittelwerte durch Cohens \(d\) berechnet werden, was definiert ist als
Der Unterschied der Mittelwerte ist im Verhältnis zu Standardabweichung also sehr klein. Die Effektstärke erweitert das Konzept der Signifikanz mit einem Maß dafür, wie groß die Differenz ist. Für normalverteilte Daten kann die Effektstärke vom Unterschied der Mittelwerte durch Cohen’s \(d\) berechnet werden, was definiert ist als
mit
Der Wert \(s\) definiert die gepoolte Standardabweichung zweier Stichproben, definiert als das nach der Anzahl der Datenpunkte gewichtete Mittel der Standardabweichungen der Stichproben. Daher ist Cohens \(d\) nichts anderes als das Verhältnis der Mittelwertdifferenz zur Standardabweichung und \(d=1\) bedeutet, dass die Mittelwerte eine Standardabweichung voneinander entfernt liegen. Basierend auf Cohen und Sawilowski kann man Table 11.1 zur Interpretation der Größenordnung der Effektstärke benutzen [3].
Cohens \(d\) |
Effektstärke |
|---|---|
\(\vert d \vert < 0.01\) |
Vernachlässigbar / Negligible |
\(\vert d \vert \geq 0.01\) |
Sehr klein / Very small |
\(\vert d \vert \geq 0.2\) |
Klein / Small |
\(\vert d \vert \geq 0.5\) |
Mittel / Medium |
\(\vert d \vert \geq 0.8\) |
Groß / Large |
\(\vert d \vert \geq 1.2\) |
Sehr groß / Very large |
\(\vert d \vert \geq 2.0\) |
Riesig / Huge |
Diese Tabelle wurde zwar für die Sozialwissenschaften erstellt, wird aber dennoch sehr häufig auch in anderen Domänen verwendet. In unserem Beispiel haben wir folgende Effektstärke:
Show code cell source
from statistics import mean, stdev
from math import sqrt
s = sqrt( ((len(s1)-1)*stdev(s1)**2 + (len(s2)-1)*stdev(s2)**2)/(len(s1)+len(s2)-2))
cohens_d = (mean(s1) - mean(s2)) / s
if abs(cohens_d)<0.01:
effsizestr = "vernachlässigbar"
elif abs(cohens_d)<0.2:
effsizestr = "sehr kleiner"
elif abs(cohens_d)<0.5:
effsizestr = "kleiner"
elif abs(cohens_d)<0.8:
effsizestr = "mittelerer"
elif abs(cohens_d)<1.2:
effsizestr = "großer"
elif abs(cohens_d)<2:
effsizestr = "sehr großer"
else:
effsizestr = "riesiger"
print("Effektstärke (Cohens d): %.3f - %s Effekt" % (cohens_d, effsizestr))
Effektstärke (Cohens d): -0.393 - kleiner Effekt
Es gibt also einen kleinen Effekt. Das passt auch zu dem, was wir im Histogramm sehen: Es gibt zwar einen Unterschied zwischen den Stichproben, der ist aber klein, wie wir jetzt mithilfe von Cohens \(d\) bestätigt haben.
11.3. Konfidenzintervalle#
Wenn man den Mittelwert anhand einer Stichprobe schätzt, ist es naheliegend, zu fragen, wie gut diese Schätzung ist. Das hängt von zwei Faktoren ab: der Größe der Stichprobe und der Variabilität der Daten. Dies erkennt man schnell an einem Beispiel: Angenommen wir wollen das Durchschnittsalter unserer Kunden bestimmen. Dass die Schätzung besser wird, je mehr Kunden wir befragen, ist offensichtlich. Wenn die ersten Kunden alle mit Zahlen zwischen 18 und 25 antworten, haben wir eine kleine Variabilität der Antworten und können den Wert schon gut eingrenzen. Wenn die ersten Kunden jedoch Zahlen zwischen 18 und 86 nennen, haben wir eine größere Unsicherheit und müssen mehr Kunden befragen, um zu einem guten Schätzwert zu kommen.
Dies ist auch für die Bewertung von Klassifikationsmodellen relevant. Angenommen wir haben ein Klassifikationsmodell für die Abwanderung von Kunden, das auf den Daten von fünf Filialen trainiert wird und mit 15 Filialen ausgewertet wird. Es gibt dann 15 Schätzwerte für die Güte dieses Modells. Als fiktive Ergebnisse nehmen wir an, dass die Accuracy normalverteilt mit einem Mittelwert von 0,83 und einer Standardabweichung von 0,13 ist. Für die weitere Anwendung ist folgende Frage sehr wichtig: Welchen Mittelwert erwarten wir, wenn wir das Modell bei 15 weiteren Filialen anwenden?
Dies kann man mithilfe von Konfidenzintervallen berechnen. Ein \(C\%\)-Konfidenzintervall \(\theta\) für einen Parameter \(p\) ist ein Intervall, in dem \(p\) mit \(C\%\) Wahrscheinlichkeit liegt. Konfidenzintervalle kann man für beliebige statistische Merkmale \(p\) berechnen, auch wenn sie meistens für den Mittelwert berechnet werden. Der wahre Wert von \(p\) liegt dann mit hoher Wahrscheinlichkeit, nämlich mit \(C\%\), in diesem Intervall. Die Wahrscheinlichkeit \(C\) nennt man das Konfidenzniveau. Für ein Konfidenzniveau von \(C=0,95\) haben wir also eine 95%-Chance, dass der Mittelwert von weiteren Stichproben im Konfidenzintervall liegt.
Für die Stichprobe \(X = \{x_1, ..., x_n\}\) einer normalverteilten Population kann man das Konfidenzintervall für den Mittelwert berechnen als
wobei \(z_C\) der sogenannte z-value des Konfidenzniveaus ist. Die Formel passt zur Intuition: Das Konfidenzintervall wird kleiner, wenn die Stichprobe größer oder die Standardabweichung kleiner ist. In der Praxis liest man den Wert \(z_C\) einfach aus einer Tabelle ab, zum Beispiel direkt aus Table 11.2.
\(C\) |
\(z_C\) |
|---|---|
90% |
1,645 |
95% |
1,96 |
99% |
2,58 |
99,5% |
2,807 |
99,9% |
3,291 |
In dieser Tabelle stehen die z-values der Standardnormalverteilung. Der z-value ist so gewählt, dass die Fläche unter der Dichtefunktion der Normalverteilung \(C\) entspricht.
Show code cell source
from math import sqrt
from scipy.stats import norm
mu = 0
sigma = 1
zc = 1.96
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
y = norm.pdf(x, mu, sigma)
xfill = np.linspace(-zc, zc)
fix, ax = plt.subplots()
ax.set_title("Dichtefunktion der Standardnormalverteilung (mean=0, sd=1)")
ax.fill_between(xfill, norm.pdf(xfill), y2=0, alpha=0.1, color='b')
ax.set_xticks([-zc,0,zc])
ax.set_xticklabels(['$-z_C$','0','$z_C$'])
ax.plot(x,y)
ax.text(-1, 0.15, "C% Wahrscheinlichkeit")
plt.show()
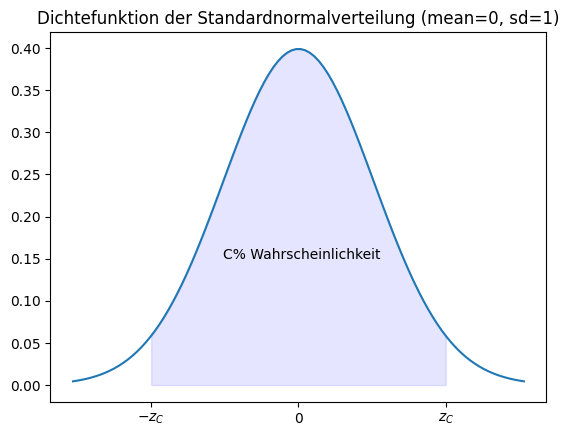
In unserem Beispiel erhalten wir für verschiedene Konfidenzlevel die folgenden Konfidenzintervalle:
Show code cell source
mymu = 0.83
mysd = 0.13
myn = 15
x = np.linspace(0.7, 0.999)
y_upper = 0.83+norm.ppf((1-x)/2)*mysd/sqrt(myn)
y_lower = 0.83-norm.ppf((1-x)/2)*mysd/sqrt(myn)
fig, ax = plt.subplots()
ax.plot()
ax.plot(x,y_upper, color='navy')
ax.plot(x,y_lower, color='navy')
ax.plot([0.7,0.999],[0.83,0.83], color='darkorange')
ax.fill_between(x, y_upper, y2=y_lower, alpha=0.1, color='b')
ax.set_title('Konfidenzintervalle für verschiedene Konfidenzniveaus\nmean=0.83, sd=0.13, n=15')
ax.set_xlabel('Konfidenzniveau')
ax.set_ylabel('Konfidenzintervall')
plt.show()
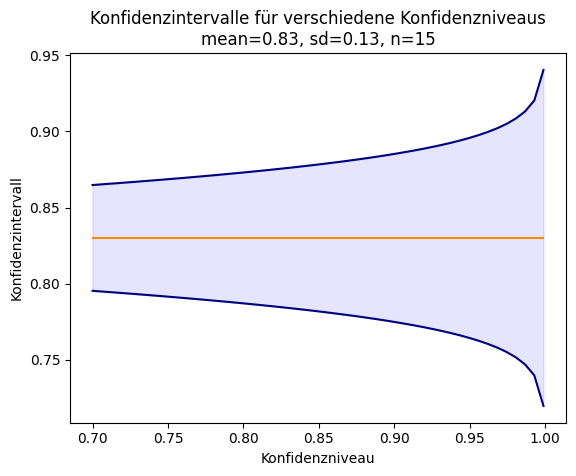
Ähnlich wie bei p-value wird auch das Konfidenzintervall häufig falsch interpre-tiert. Hier sind einige korrekte Interpretationen eines \(C\%\)-Konfidenzintervalls:
Es gibt eine \(C\%\)-Chance, dass der gemessene Wert (zum Beispiel Mittelwert) bei zukünftigen Wiederholungen des gleichen Experiments in das Intervall \(\theta\) fällt.
Es gibt keinen statistisch signifikanten Unterschied zwischen dem geschätzten Wert und allen Werten in \(\theta\) mit einem Signifikanzniveau von \(1-C\%\).
Es gibt eine \(1-C\%\)-Wahrscheinlichkeit der Stichprobe, wenn der wahre Wert außerhalb des Intervalls \(\theta\) liegt.
Übliche falsche Interpretationen des Konfidenzintervalls sind zum Beispiel:
Der wahre Wert von \(p\) liegt mit \(C\%\) Wahrscheinlichkeit in \(\theta\). Ähnlich wie beim p-value bei Hypothesentests liefern Konfidenzintervalle nur eine Aussage über die Wahrscheinlichkeit bei Stichproben.
\(C\%\) der beobachteten Daten liegen innerhalb von \(\theta\). Hier wird das Konfidenzintervall mit den Quantilen verwechselt.
11.4. Gute Beschreibung von Ergebnissen#
In der Wissenschaft, aber auch in der Praxis, wird häufig nur geschaut, ob es Unterschiede gibt und eventuell noch ob diese signifikant sind. Eine saubere statistische Bewertung von Projektergebnissen sollte aber darüber hinaus gehen und zum Beispiel auch die Effektstärke und die Konfidenzintervalle beinhalten. Außerdem sollte man die statistische Auswertung zu Beginn eines Projekts planen. Andernfalls riskiert man das oben beschriebene p-Hacking, indem man Experimente immer weiter anpasst, bis man ein gewünschtes Ergebnis gefunden hat. In der Wissenschaft führt dies zur Registrierung von Studien, bei denen das Protokoll bereits vor der Durchführung festgelegt wird. Dieses Vorgehen hat sich bereits bei klinischen Studien in der Medizin bewährt und vermeidet falsch-positive Ergebnisse.
In diesem Kapitel haben wir uns nur mit der häufigkeitsbasierten Statistik beschäftigt. Es gibt auch noch einen anderen Ansatz, die Bayesian Statistik, die im Kern auf dem Satz von Bayes (siehe Kapitel 7) basiert. Hier wird direkt geschätzt, wie wahrscheinlich es ist, dass eine Hypothese wahr ist. Dies hat den Vorteil, dass die Ergebnisse einfacher zu interpretieren sind. Die Theorie und Anwendung ist hier jedoch etwas komplexer, weshalb die häufigkeitsbasierte Statistik weiterhin bei vielen Analysen das Mittel der Wahl ist.
11.5. Übung#
In dieser Übung wenden wir die eingeführten statistischen Methoden zum besseren Verständnis an. Hierzu vergleichen wir verschiedene Klassifikationsmodelle auf den Irisdaten [4].
11.5.1. Mehrfaches Training#
Erstellen Sie fünf zufällige Aufteilungen der Irisdaten in je 50% Trainingsdaten und 50% Testdaten. Trainieren Sie ein 5-Nearest-Neighbor-Modell und einen Random Forest (mit 100 Random Trees) für jede dieser Aufteilungen. Berechnen Sie die Güte für jedes dieser Modelle mit MCC und erstellen Sie für jedes Modell eine Liste mit den Ergebnissen.
11.5.2. Statistischer Vergleich#
Vergleichen Sie das arithmetische Mittel, die Standardabweichung, den Median, das Minimum und das Maximum des MCC für beide Algorithmen. Benutzen Sie geeignete statistische Tests, um zu bestimmen, ob der Unterschied signifikant ist. Falls der Unterschied signifikant ist, berechnen Sie Cohens \(d\), um die Effektstärke zu bestimmen. Berechnen Sie außerdem das 95%-Konfidenzintervall des arithmetischen Mittels von MCC.
11.5.3. Mehr Vergleiche#
Wiederholen Sie diese Auswertung mit 10, 50 und 100 zufälligen Aufteilungen der Irisdaten. Wie verändern sich die Ergebnisse?
