5. Assoziationsregeln#
Assoziationen sind Beziehungen zwischen Objekten. Die Idee hinter den Assoziationsregeln besteht darin, diese Beziehungen durch Regeln so zu beschreiben, dass wir erkennen können, welche weiteren Objekte zu den bisherigen Objekten passen. Bei den Assoziationsregeln spricht man statt von Objekten in der Regel von Gegenständen (engl. items). Fig. 5.1 zeigt das Standardbeispiel für Assoziationsregeln: die Analyse von Warenkörben bei Einkäufen. Ein Kunde fügt Produkte (Gegenstände) dem Warenkorb hinzu. Sobald der Warenkorb nicht mehr leer ist, kann man den Inhalt nutzen, um Assoziationen zu weiteren Produkten, die für den Kunden von Interesse sind, herzustellen. Diese können dem Kunden dann zum Beispiel als Werbung vorgeschlagen werden.
Fig. 5.1 Warenkörbe als Beispiel für Assoziationen#
In diesem Beispiel sind die Assoziationen definiert als “Produkte, die von Kunden gleichzeitig gekauft werden”. Wenn man dies generalisiert, hat man Transaktionen, wobei jede Transaktion eine Beobachtung von gemeinsam verarbeiteten Gegenständen ist. Mithilfe der Assoziationsanalyse werden Assoziationsregeln aus den Transaktionen gelernt. Dies wird in Fig. 5.2 gezeigt.
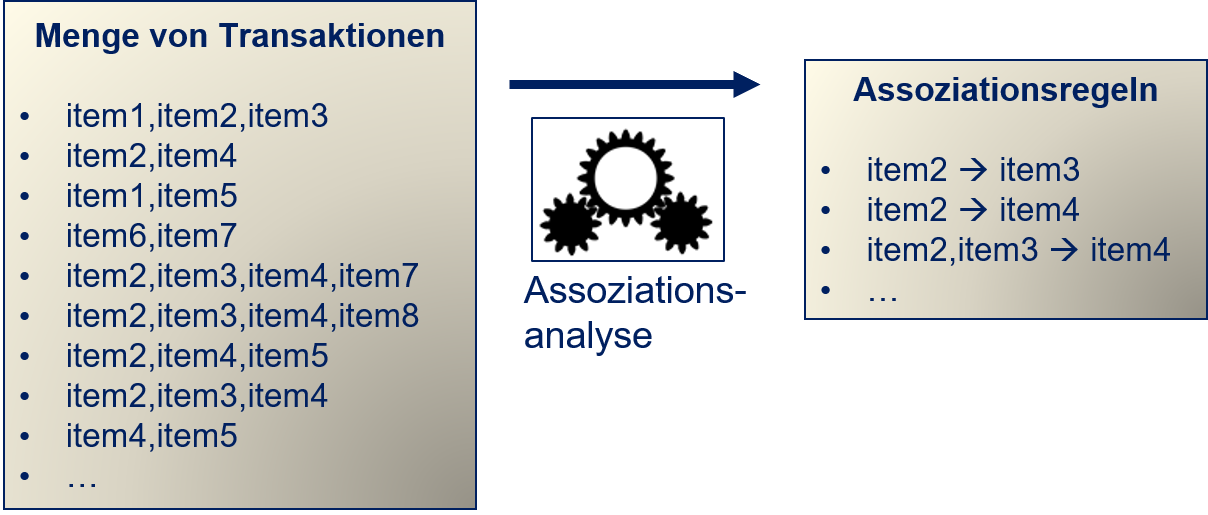
Fig. 5.2 Konzept der Assoziationsanalyse#
Die Assoziationsregeln sollten “interessante” Beziehungen beschreiben. Die Definition von interessant hängt vom Anwendungsfall ab. Im obigen Beispiel sind Beziehungen interessant, die beschreiben, was Kunden bewusst zusammen kaufen. Wir können die Assoziationsanalyse auch formal definieren. Gegeben ist eine Menge von Gegenständen, auch Itemsets genannt, definiert als \(I = \{i_1, ..., i_m\}\), und eine Menge von Transaktionen \(T = \{t_1, ..., t_n\}\), wobei jede Transaktion eine Teilmenge von Gegenständen beinhaltet, also \(t_j \subseteq I, j=1, ..., n\). Assoziationsregeln sind logische Ausdrücke der Form \(X \Rightarrow Y\), wobei \(X\) und \(Y\) disjunkte Teilmengen von Gegenständen sind, d.h., es gilt \(X, Y \subseteq I\) und \(X \cap Y = \emptyset\). Man nennt \(X\) auch Bedingung (engl. antecedent) oder linke Seite der Regel und \(Y\) auch Folgerung (engl. consequent) oder rechte Seite der Regel.
Bemerkung:
Ihnen ist möglicherweise aufgefallen, dass wir bisher keine Merkmale benannt haben, sondern stattdessen von Gegenständen gesprochen haben. Außerdem gibt es auch keine Instanzen, sondern Transaktionen. Hierfür gibt es zwei Gründe: Zum einen ist das die übliche Terminologie der Assoziationsanalyse. Zum anderen gibt es keine echten Merkmale, da jedes Objekt durch seine Identität identifiziert wird.
Das Ziel der Assoziationsanalyse ist es, gute Assoziationsregeln zu finden, basierend auf einer Menge von Transaktionen. Eine generische Definition von “interessante Beziehung” besteht darin, dass Gegenstände häufig zusammen in Transaktionen auftreten. Hier ist ein Beispiel mit zehn Transaktionen.
Show code cell source
# we define each transaction as a list
# a set of transactions is a list of lists
data = [['item1', 'item2', 'item3'],
['item2', 'item4'],
['item1', 'item5'],
['item6', 'item7'],
['item2', 'item3', 'item4', 'item7'],
['item2', 'item3', 'item4', 'item8'],
['item2', 'item4', 'item5'],
['item2', 'item3', 'item4'],
['item4', 'item5'],
['item6', 'item7']]
print('Transaktionen (eine pro Zeile):')
print('\n'.join([str(t) for t in data]))
Transaktionen (eine pro Zeile):
['item1', 'item2', 'item3']
['item2', 'item4']
['item1', 'item5']
['item6', 'item7']
['item2', 'item3', 'item4', 'item7']
['item2', 'item3', 'item4', 'item8']
['item2', 'item4', 'item5']
['item2', 'item3', 'item4']
['item4', 'item5']
['item6', 'item7']
In diesem Beispiel tauchen die Gegenstände item2, item3 und item4 oft zusammen auf, was auf eine interessante Beziehung hindeutet. Im Folgenden erklären wir, wie man effizient solche Beziehungen findet, hieraus Regeln erstellt und die Güte der Regeln bewertet.
5.1. Der Apriori-Algorithmus#
Der Apriori-Algorithmus ist ein vom Prinzip sehr einfacher, aber dennoch mächtiger Algorithmus, um Assoziation in Daten zu suchen.
5.1.1. Support und Frequent Itemsets#
Der Apriori-Algorithmus basiert auf dem Konzept des Supports von Itemsets \(IS \subseteq I\). Der Support eines Itemsets \(IS\) ist definiert als der Anteil der Transaktionen, in denen alle Gegenstände des Itemsets vorkommen. Es gilt also:
Der Support ist sehr ähnlich zur generischen Definition von “interessanten Beziehungen”, die wir oben eingeführt haben, da der Support ein Maß für die Häufigkeit ist, mit der Kombinationen von Gegenständen auftauchen. Entsprechend kann man den Support als indirektes Maß für die Interessantheit sehen. Was noch fehlt ist ein Mindestmaß an Interessantheit, sodass eine Kombination von Gegenständen relevant genug ist, um diese als Grundlage für Assoziationsregeln zu nutzen. Es ist nur logisch, dass man hierfür einen Grenzwert für den Support festlegt: Ist dieser Grenzwert überschritten, ist ein Itemset interessant und wir sprechen von einem Frequent Itemset. Formal nennen wir ein Itemset \(IS\) frequent, wenn Folgendes gilt:
für einen Grenzwert \(minsupp \in [0,1].\)
Im obigen Beispiel hat das Itemset der Gegenstände item2, item3 und item4 einen Support von
\(support(\{item2, item3, item4\}) = \frac{3}{10}\),
da alle drei Gegenstände zusammen in drei von zehn Transaktionen vorkommen. Wenn wir also \(minsupp=0,3\) wählen, wäre das Itemset \(\{item2, item3, item4\}\) ein Frequent Itemset. Insgesamt finden wir mit diesem Grenzwert die folgenden Frequent Itemsets.
Show code cell source
# we need pandas and mlxtend for the association rules
import pandas as pd
from mlxtend.frequent_patterns import apriori
from mlxtend.preprocessing import TransactionEncoder
pd.set_option('styler.render.repr', 'latex')
# we first need to create a one-hot encoding of our transactions
te = TransactionEncoder()
te_ary = te.fit_transform(data)
data_df = pd.DataFrame(te_ary, columns=te.columns_)
# we can use this function to determine all itemsets with at least 0.3 support
# what apriori is will be explained later
frequent_itemsets = apriori(pd.DataFrame(data_df), min_support=0.3, use_colnames=True)
frequent_itemsets
| support | itemsets | |
|---|---|---|
| 0 | 0.6 | (item2) |
| 1 | 0.4 | (item3) |
| 2 | 0.6 | (item4) |
| 3 | 0.3 | (item5) |
| 4 | 0.3 | (item7) |
| 5 | 0.4 | (item3, item2) |
| 6 | 0.5 | (item2, item4) |
| 7 | 0.3 | (item3, item4) |
| 8 | 0.3 | (item3, item2, item4) |
5.1.2. Ableiten von Regeln#
Ein Frequent Itemset ist noch keine Assoziationsregel, da es weder eine Bedingung \(X\) noch eine Folgerung \(Y\) gibt, aus denen eine Regel \(X \Rightarrow Y\) entsteht. Man kann jedoch relativ einfach solche Regeln aus den Frequent Itemsets ableiten. Hierzu betrachtet man alle möglichen Partitionierungen eines Frequent Itemsets, also alle Kombinationen \(X, Y \subset IS\), sodass \(X \cup Y = IS\) (jeder Gegenstand kommt in X oder Y vor) und \(X \cap Y = \emptyset\) (kein Gegenstand kommt in X und Y vor).
Im unserem Beispiel können wir acht Regeln aus dem Itemset \(\{item2, item3, item4\}\) ableiten.
from mlxtend.frequent_patterns import association_rules
association_rules(frequent_itemsets.iloc[8:9, :], metric="confidence",
min_threshold=0.0, support_only=True)[['antecedents', 'consequents']]
| antecedents | consequents | |
|---|---|---|
| 0 | (item3, item2) | (item4) |
| 1 | (item3, item4) | (item2) |
| 2 | (item2, item4) | (item3) |
| 3 | (item3) | (item2, item4) |
| 4 | (item2) | (item3, item4) |
| 5 | (item4) | (item3, item2) |
Es gibt noch zwei weitere Regeln, wenn wir die leere Menge als Bedingung oder Folgerung zulassen:
\(\emptyset \Rightarrow \{item2, item3, item4\}\)
\(\{item2, item3, item4\} \Rightarrow \emptyset\)
Diese Regeln erlauben aber keine bedeutenden Einblicke, sodass wir sie ignorieren können.
5.1.3. Confidence, Lift und Leverage#
Eine noch ungeklärte Frage ist, wie wir erkennen, welche der Regeln gut sind, oder ob alle Regeln, die man aus einem Frequent Itemset ableitet, gleich gut sind. Am Beispiel der leeren Menge sieht man recht schnell, dass vermutlich nicht alle Regeln gleich gut sind. Was wir brauchen, sind Gütemaße, die es uns erlauben, zwischen bedeutungsvollen Assoziationen und zufälligen Effekten zu unterscheiden. Hierfür ist der Support nicht ausreichend. Stellen Sie sich zum Beispiel vor, dass es etwas gratis gibt. Die Gratisprodukte werden häufig einfach “mitgenommen” und landen entsprechend oft im Warenkorb und später dann in unseren Transaktionen. Diese Gratisprodukte haben einen hohen Support und sind mit hoher Wahrscheinlichkeit ein Teil vieler Frequent Itemsets. Die Gratisprodukte sind aber nicht mit dem Rest vom Einkauf assoziiert, die Beziehung ist also zufällig. Eine Schwäche des Supports ist, dass dieser nicht von der Regel abhängt, insbesondere ist der Support einer Regel \(X \Rightarrow Y\) immer gleich der Regel \(Y \Rightarrow X\), in der Bedingung und Folgerung vertauscht sind. Da aber kausale Zusammenhänge häufig eine Richtung haben, macht diese Symmetrie in vielen Fällen keinen Sinn. Es ist zum Beispiel sinnvoll, einem Kunden, der eine Spielekonsole in den Warenkorb legt, ein Spiel für diese Konsole vorzuschlagen. Wenn jemand aber ein Spiel in den Warenkorb legt, ist die Konsole im Normalfall bereits vorhanden, und es würde keinen Sinn machen, diese vorzuschlagen.
Die Maße Confidence, Lift und Leverage helfen zu erkennen, ob Regeln zufällig sind oder ob es sich um sinnvolle Assoziationen handelt. Die Confidence ist definiert als
Es handelt sich bei der Confidence also um das Verhältnis, die Bedingung \(X\) und die Folgerung \(Y\) zusammen in einer Transaktion zu sehen, zu der Beobachtung von Transaktionen nur mit der Bedingung \(X\). Eine hohe Confidence deutet darauf hin, dass eine Bedingung selten ohne die Folgerung zu beobachten ist, was auf einen starken Zusammenhang hinweist.
Der Lift ist definiert als
Der Lift misst das Verhältnis der Erwartung, die Bedingung \(X\) und die Folgerung \(Y\) zusammen zu beobachten, im Verhältnis zur Erwartung, dass \(X\) und \(Y\) unabhängig voneinander auftauchen. Der Support kann auch als Schätzung für den Erwartungswert für ein Itemset, ein Itemset zu beobachten, interpretiert werden. Daher ist \(support(X \cup Y)\) ist nichts anderes als der Erwartungswert von \(X\) und \(Y\) zusammen und \(support(X) \cdot support(Y)\) der Erwartungswert unter der Annahme, dass \(X\) und \(Y\) unabhängig voneinander sind. Unabhängigkeit ist das direkte Gegenteil von assoziiert. Es folgt daraus, dass der Lift misst, wie viel wahrscheinlicher es ist, dass die Teile einer Regel \(X\) und \(Y\) in irgendeiner Weise voneinander abhängen, als dass diese unabhängig sind. Ein Lift von 2 bedeutet also, dass eine Assoziation von X und Y doppelt so wahrscheinlich ist, wie dass es keine gibt.
Der Leverage ist definiert als
Diese Definition ist ähnlich zum Lift, nur dass die Differenz statt des Verhältnisses betrachtet wird. Entsprechend gibt es eine enge Beziehung zwischen Lift und Leverage. Der Unterschied besteht darin, dass Leverage tendenziell höhere Werte für Itemsets mit einem hohen Support liefert.
Um Confidence, Lift und Leverage besser zu verstehen, betrachten wir diese nun am Beispiel der Regeln, die wir aus dem Itemset \(\{item2, item3, item4\}\) ableiten können.
Show code cell source
# all rules for our data
# we drop the column conviction, because this metric is not covered here
# we also drop all rules from other itemsets than above.
association_rules(frequent_itemsets, metric="confidence",
min_threshold=0.0).drop('conviction', axis=1)[6:].reset_index(drop=True)
| antecedents | consequents | antecedent support | consequent support | support | confidence | lift | leverage | zhangs_metric | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (item3, item2) | (item4) | 0.4 | 0.6 | 0.3 | 0.75 | 1.250000 | 0.06 | 0.333333 |
| 1 | (item3, item4) | (item2) | 0.3 | 0.6 | 0.3 | 1.00 | 1.666667 | 0.12 | 0.571429 |
| 2 | (item2, item4) | (item3) | 0.5 | 0.4 | 0.3 | 0.60 | 1.500000 | 0.10 | 0.666667 |
| 3 | (item3) | (item2, item4) | 0.4 | 0.5 | 0.3 | 0.75 | 1.500000 | 0.10 | 0.555556 |
| 4 | (item2) | (item3, item4) | 0.6 | 0.3 | 0.3 | 0.50 | 1.666667 | 0.12 | 1.000000 |
| 5 | (item4) | (item3, item2) | 0.6 | 0.4 | 0.3 | 0.50 | 1.250000 | 0.06 | 0.500000 |
Basierend auf den Metriken schneidet die Regel \(\{item3, item4\} \Rightarrow \{item2\}\) klar am besten ab. Diese Regel hat eine perfekte Confidence von 1, was nichts anderes bedeutet, als dass item2 in jeder Transaktion vorkommt, in der item3 und item 4 zusammen vorkommen. Der Lift von 1,66 besagt, dass dieses gemeinsame Auftreten 1,66-mal wahrscheinlicher ist, als es sich durch eine zufällige Beziehung erklären lässt. Hier sieht man auch den Unterschied zur Regel \(\{item2\} \Rightarrow \{item3, item4\}\), also der Regel, die wir bekommen, wenn wir Bedingung und Folgerung vertauschen. Diese Regel hat zwar den gleichen Lift (und Leverage), die Confidence ist jedoch nur 0,5. Das bedeutet, dass item2 genauso häufig alleine vorkommt wie mit item3 und item4 zusammen. Während also die Regel \(\{item3, item4\} \Rightarrow \{item2\}\) vermutlich fast jedes Mal richtig ist, ist die Regel \(\{item2\} \Rightarrow \{item3, item4\}\) in ca. der Hälfte der Fälle falsch.
Das Beispiel zeigt auch die grundlegenden Eigenschaften der drei Maße: Lift und Leverage sind symmetrisch, genauso wie der Support. Die Confidence ist das einzige Gütemaße, das berücksichtigt, welcher Teil einer Regel die Bedingung und welcher Teil die Folgerung ist, also das einzige Maß, das die Kausalität einbezieht. Daher sollte man die Confidence immer bei der Bewertung von Regeln benutzen. Da Lift und Leverage sich sehr ähnlich verhalten, reicht es, nur eines der beiden Maße zu verwenden. Legt man mehr Wert auf Regeln, die aus Itemsets mit hohem Support gewonnen werden, ist Leverage besser, ansonsten sollte man Lift wählen. Der Grund hierfür ist, dass es für Lift eine direkte Interpretation gibt, also wie viel wahrscheinlicher etwas ist, als es sich durch den reinen Zufall erklären lässt.
5.1.4. Exponentielles Wachstum#
Oben haben wir gezeigt, wie wir Assoziationsregeln bestimmen können: Wir müssen die Frequent Itemsets finden, aus denen wir dann Regeln ableiten können. Das Finden von Frequent Itemsets ist jedoch leider nicht trivial. Das Problem ist das exponentielle Wachstum der Itemsets mit der Anzahl von Gegenständen. Die Anzahl von möglichen Itemsets ist die Potenzmenge \(\mathcal{P}\) von \(I\), also die Menge aller möglichen Kombinationen von Gegenständen. Daher gibt es \(\mathcal{P}(I)=2^{|I|}\) Itemsets. Es ist aber gar nicht sinnvoll, beliebig lange Kombinationen von Gegenständen zu betrachten. Zu lange Regeln würden bedeuten, dass man diese nur in wenigen Fällen anwenden kann. Daher ist man häufig nur an relativ kurzen Regeln interessiert. Leider ist das Wachstum auch mit einer beschränkten Anzahl von Gegenständen in Itemsets noch exponentiell. Hierzu können wir den Binomialkoeffizienten
nutzen, um die Anzahl der Itemsets der Größe \(k\) zu berechnen. Wenn wir zum Beispiel \(|I|=100\) Gegenstände haben, gibt es 161.700 Itemsets der Größe \(k=3\). Aus jedem dieser Itemsets können wir sechs Regeln ableiten, ohne dass die Bedingung oder Folgerung die leere Menge ist, es gibt also 970.200 mögliche Regeln.
Es ist also nicht möglich, einfach alle Itemsets zu berechnen und erst anschließend die Frequent Itemsets zu bestimmen. Wir brauchen stattdessen einen Algorithmus, der die exponentielle Natur des Problems beschränkt und der schonend mit den vorhandenen Ressourcen umgeht, da sonst schnell der Speicher ausgeht oder die Rechenzeit zu lang wird.
5.1.5. Die Apriori-Eigenschaft#
Die Apriori-Eigenschaft verleiht dem Algorithmus seinen Namen.
Apiori-Eigenschaft
Sei \(IS \subseteq I\) ein Frequent Itemset. Alle Teilmengen \(IS' \subseteq IS\) sind auch Frequent Itemsets und es gilt \(support(IS') \geq support(IS)\).
Wir können die Apriori-Eigenschaft nutzen, um gezielt nach Frequent Itemsets zu suchen und damit den Suchraum zu beschränken. Anstatt alle Itemsets zu berechnen und dann zu überprüfen, ob es Frequent Itemsets sind, lassen wir die Frequent Itemsets wachsen. Da alle Teilmengen eines Frequent Itemsets ebenfalls Frequent Itemsets sind, wissen wir auch, dass ein Itemset, das eine Teilmenge hat, die kein Frequent Itemset ist, kein Frequent Itemset sein kann. Basierend auf dieser Beobachtung können wir folgenden Algorithmus definieren:
Berechne den Support für alle Itemsets der Größe \(k=1\).
Entferne alle Itemsets, die nicht den minimalen Support haben, sodass nur Frequent Itemsets übrig sind.
Erstelle alle möglichen Kombinationen der Größe \(k+1\) aus den Frequent Itemsets der Größe \(k\).
Setze \(k=k+1\) und wiederhole die Schritte 2 und 3, bis
es keine Itemsets der Größe \(k+1\) gibt oder
ein Grenzwert für \(k\) erreicht ist, also die maximale Länge von Itemsets.
Wir lassen also die Frequent Itemsets Stück für Stück wachsen und ignorieren alle Itemsets bei der Überprüfung, ob sie frequent sind, die nicht die Apriori-Eigenschaft erfüllen. Dieser Algorithmus ist immer noch exponentiell. Es könnten zum Beispiel alle Transaktionen alle Gegenstände beinhalten. In dem Fall wären alle ein Frequent Itemset und man hätte immer noch exponentielles Wachstum. In der Praxis passiert das jedoch sehr selten, sodass der Algorithmus in der Regel gut skaliert, sofern der Support hinreichend hoch gewählt wird.
Um den Algorithmus besser zu verstehen, sehen wir uns an, wie man die Frequent Itemsets für \(minsupp=0,3\) für unsere Beispieldaten bestimmt. Hier sind noch einmal die Daten:
Show code cell source
print('Transaktionen (eine pro Zeile):')
print('\n'.join([str(t) for t in data]))
Transaktionen (eine pro Zeile):
['item1', 'item2', 'item3']
['item2', 'item4']
['item1', 'item5']
['item6', 'item7']
['item2', 'item3', 'item4', 'item7']
['item2', 'item3', 'item4', 'item8']
['item2', 'item4', 'item5']
['item2', 'item3', 'item4']
['item4', 'item5']
['item6', 'item7']
Zuerst betrachten wir den Support der einzelnen Gegenstände in Table 5.1.
Itemsets |
support |
Entfernen |
|---|---|---|
\(\{item1\}\) |
0.2 |
x |
\(\{item2\}\) |
0.6 |
|
\(\{item3\}\) |
0.4 |
|
\(\{item4\}\) |
0.5 |
|
\(\{item5\}\) |
0.3 |
|
\(\{item6\}\) |
0.2 |
x |
\(\{item7\}\) |
0.3 |
|
\(\{item8\}\) |
0.1 |
x |
Da die Gegenstände item1, item6 und item8 nicht den minimalen Support von 0,3 haben, können wir diese entfernen und müssen keine Itemsets der Größe \(k=2\) mit diesen Gegenständen betrachten. Table 5.2 zeigt die Itemsets für \(k=2\).
Itemsets |
support |
Entfernen |
|---|---|---|
\(\{item2, item3\}\) |
0.4 |
|
\(\{item2, item4\}\) |
0.5 |
|
\(\{item2, item5\}\) |
0.1 |
x |
\(\{item2, item7\}\) |
0.1 |
x |
\(\{item3, item4\}\) |
0.3 |
|
\(\{item3, item5\}\) |
0.0 |
x |
\(\{item3, item7\}\) |
0.1 |
x |
\(\{item4, item5\}\) |
0.2 |
x |
\(\{item4, item7\}\) |
0.1 |
x |
\(\{item5, item7\}\) |
0.0 |
x |
Wie man sieht, sind die Kombinationen der Gegenstände item2, item3 und item4 in Frequent Itemsets. Alle anderen Items müssen also bei der Größe \(k=3\) nicht weiter betrachtet werden. Daher gibt es nur noch ein Itemset, das wir in Table 5.3 sehen.
Itemset with \(k=3\) |
support |
Entfernen |
|---|---|---|
\(\{item2, item3, item4\}\) |
0.3 |
Da es keine weiteren Itemsets mit \(k=4\) Gegenständen gibt, sind wir fertig. Insgesamt musste der Support von \(8+10+1=19\) Itemsets ausgerechnet werden, um alle Frequent Itemsets aus den \(2^8=256\) möglichen Itemsets zu finden. Wir konnten also den Aufwand um 93% reduzieren, indem wir die Apriori-Eigenschaft ausgenutzt haben.
5.1.6. Einschränkungen für Regeln#
Bisher haben wir alle möglichen Kombinationen aus Bedingung und Folgerung, die wir aus einem Itemset bilden können, betrachtet und lediglich die leere Menge wurde verworfen. Für viele Anwendungsfälle ist eine weitere Einschränkung sinnvoll: Nur Regeln, deren Folgerung aus einem Gegenstand bestehen, werden betrachtet. Der Vorteil derartiger Regeln ist, dass die Grundlage für die Folgerung “besser” ist, da die Bedingung länger ist. Hierdurch ist es wahrscheinlicher, dass eine Regel gut ist.
5.2. Bewertung von Assoziationsregeln#
Nachdem man Assoziationsregeln bestimmt hat, muss man im letzten Schritt ihre Güte bewerten, also ob es sich um echte Assoziationen oder um zufällige Zusammenhänge handelt. Die Gütemaße Confidence, Lift und Leverage sind bereits ein guter erster Schritt, um Regeln zu bewerten, insbesondere wenn sie gemeinsam betrachtet werden. Die Confidence beschreibt, ob die Beziehung zufällig ist, weil die Bedingung oft beobachtet wird. Lift und Leverage geben an, ob die Beziehung selbst häufiger als durch den Zufall erklärbar beobachtet wird.
Die Betrachtung dieser Gütemaße sollte jedoch nicht das einzige Kriterium bei der Bewertung von Regeln sein. Zum einen sollte man auch bei Assoziationsregeln mit Trainings- und Testdaten arbeiten. Auf den Testdaten kann man überprüfen, ob die gleichen Regeln gefunden werden. Falls die Überschneidung groß ist, ist das ein Indikator, dass die Regeln generalisieren. Man kann auch noch einen Schritt weiter gehen und in den Testdaten zufällig Gegenstände aus Warenkörben entfernen und überprüfen, wie häufig die Regeln diese fehlenden Gegenstände richtig vorhersagen würden.
Neben der Auswertung der Güte auf den Daten sollte man die Regeln auch manuell bewerten: Findet eine Domänenexpertin die Regeln sinnvoll? Jeder, der regelmäßig in Webshops einkauft, wird sich schon das ein oder andere Mal über seltsame Empfehlungen gewundert haben. Hier wurde in der Regel außergewöhnliches Kaufverhalten gelernt und die Regeln nicht ausreichend validiert. Durch eine manuelle Inspektion der Regeln kann man das Ergebnis daher normalerweise verbessern und das Regelwerk filtern. Dies ist eine Aufgabe, die man als Data Scientist nicht alleine angehen sollte, sondern immer zusammen mit Domänenexpertinnen.
5.3. Übung#
Prüfen Sie Ihr Wissen über Assoziationsregeln in einer praktischen Übung. Lernen Sie hierbei Assoziationsregeln aus einem Datensatz aus einem Supermarkt [1]. Zum Lesen der Daten können Sie folgenden Quelltext nutzen.
with open('data/store_data.csv') as f:
records = []
for line in f:
records.append(line.strip().split(','))
5.3.1. Finden von Frequent Itemsets#
Nutzen Sie den Apriori-Algorithmus, um Frequent Itemsets zu finden. Hierzu müssen Sie auch einen geeigneten Grenzwert für den Support bestimmen. Begründen Sie Ihre Wahl.
5.3.2. Erstellen von Regeln#
Erstellen Sie Regeln aus den Frequent Itemsets. Nutzen Sie Lift und Confidence, um zu ermitteln, welche Regeln gut sind.
5.3.3. Validieren der Regeln#
Teilen Sie die Daten zufällig in zwei Datensätze mit je 50% der Transaktionen auf. Wenden Sie den Apriori-Algorithmus auf beide Datensätze an, um Regeln zu bestimmen. Vergleichen Sie die gefundenen Regeln miteinander sowie mit den Regeln, die Sie auf allen Daten gefunden haben. Welche Unterschiede gibt es? Was bedeuten die Unterschiede?
